
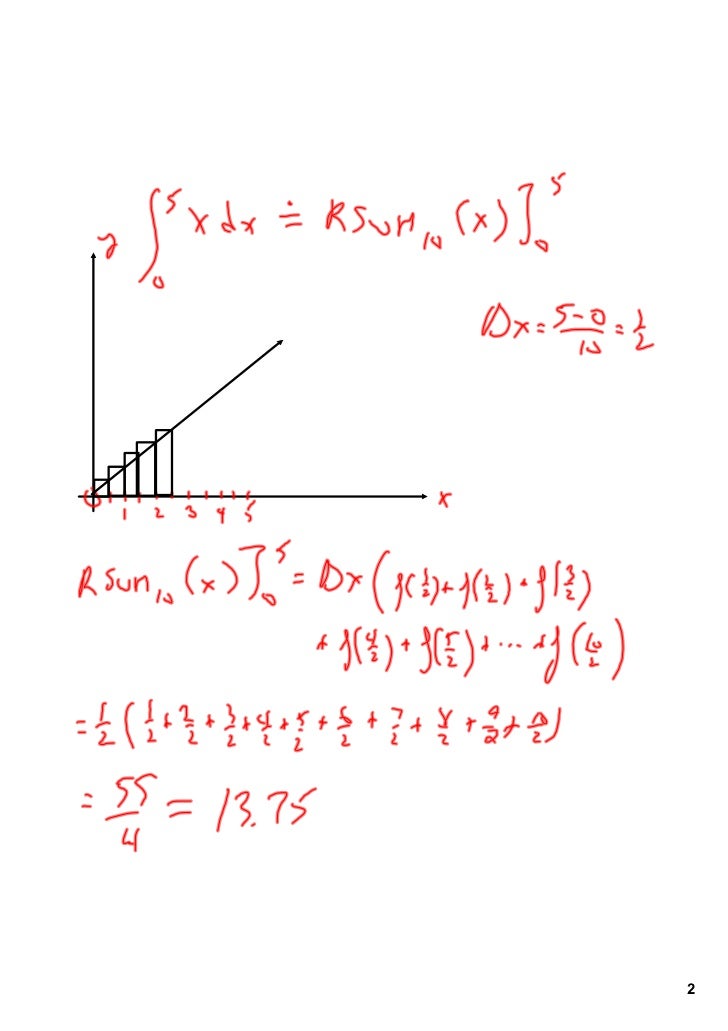
Now we need to find the x values that are the left endpoints of each of the 4 subintervals. We then split this total length into 4 pieces, since we are told to use 4 subintervals.

To find we find the total length between the beginning and ending x values, which are given in the problem as and. This is basically, 4 times, and then added together. Think of as the base of each box, and as the height of the 1st box. We can rewrite this fancy equation by writing, 4 times 1 time each for, ,, and. This fancy equation approximates using boxes. , is the width of each subinterval, which we will determine shortly.Īnd means add all versions together (for us that means add up 4 versions). Is the function value when you plug in the "i-th" x value, (i-th in this case will be 1-st, 2-nd, 3-rd, and 4-th) Is the "counter" that denotes which subinterval we are working with,(4 subintervals mean that will be 1, 2, 3, and then 4) Where is the number of subintervals, (4 in our problem), The best way to prepare for this challenging exam is to complete as many practice problems and exams as possible.To use left Riemann sums, we need to use the following formula: Part B consists of four problems in which a calculator is not permitted.īoth the multiple choice and free response questions expect you to evaluate, analyze, conceptualize, and develop functions and representations both at face value in in real-world contexts. Part A has two free response questions that require a graphing calculator. Section II is also broken down into a Part A and Part B, but the calculator usage is reversed. Part A does not allow a graphing calculator and Part B allows a graphing calculator, with some questions requiring its use in order to get an answer.

Section I is further broken down into Part A and Part B. Section II is the free response section which you have 90 minutes to complete. Section I is the multiple choice section which you have 105 minutes to complete. The AP Calculus AB exam is divided into two sections, each worth 50% of your final score.


 0 kommentar(er)
0 kommentar(er)
